用 Python 从头实现神经网络

Fermi included in IT

2024-07-04 5646 words 12 minutes

Contents

原文地址：Machine Learning for Beginners: An Introduction to Neural Networks

有个事情可能会让初学者惊讶：神经网络并不复杂！『神经网络』这个词让人觉得很高大上，但实际上神经网络算法要比人们想象的简单。

这篇文章完全是为新手准备的。我们会通过用Python从头实现一个神经网络来理解神经网络的原理。

砖块：神经元

首先让我们看看神经网络的基本单位，神经元。神经元接受输入，对其做一些数据操作，然后产生输出。例如，这是一个2-输入神经元：

这里发生了三个事情。首先，每个输入都跟一个权重相乘（红色）：

$$ x_{1}→x_{1}× w_{1} $$$$ x_{2}→x_{2}× w_{2} $$$$ (x_{1}× w_{1})+(x_{2}× w_{2})+b $$

最后，这个结果传递给一个激活函数 $f$：

$$ y=f((x_{1}× w_{1})+(x_{2}× w_{2})+b) $$

激活函数的用途是将一个无边界的输入，转变成一个可预测的形式。常用的激活函数就就是S型函数：

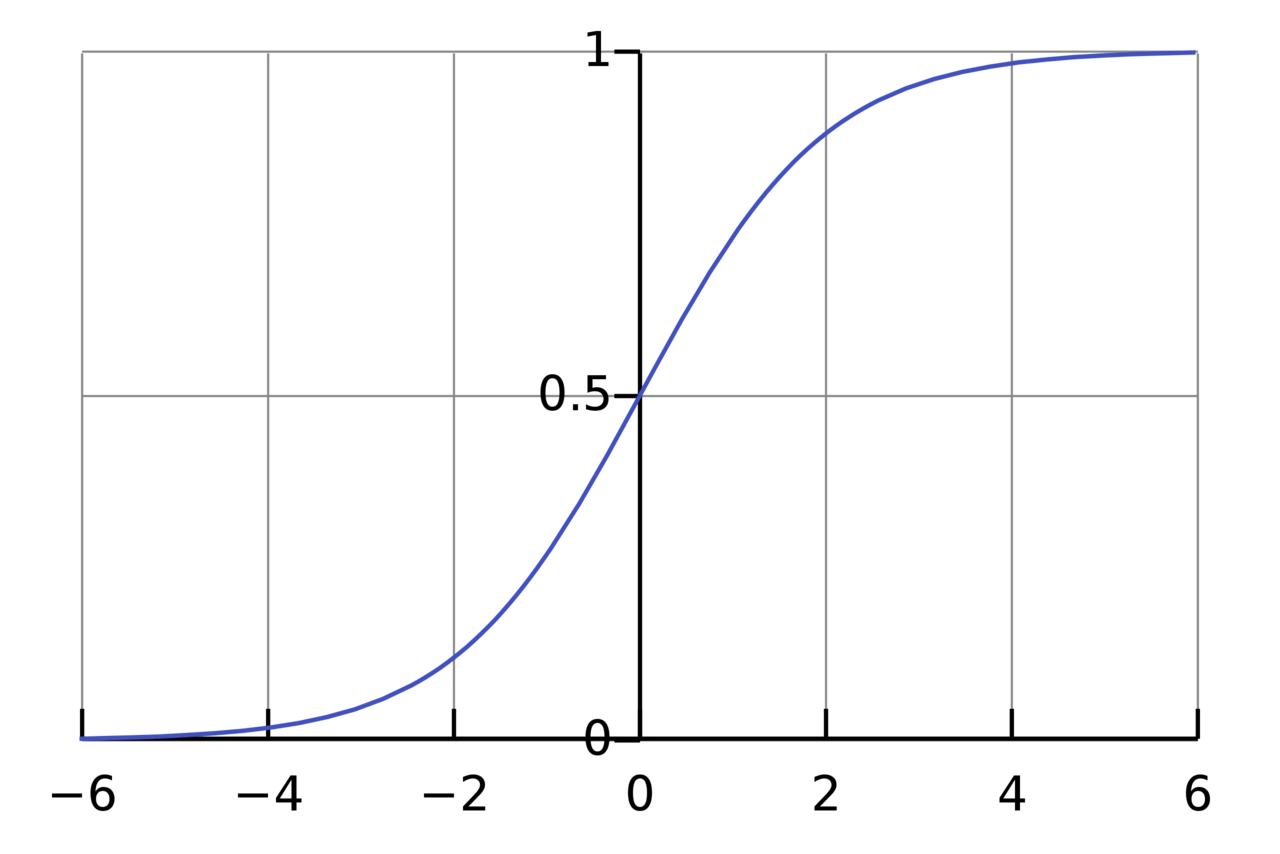
S 型函数的值域是 $(0, 1)$。简单来说，就是把 $(−∞, +∞)$ 压缩到 $(0, 1)$ ，很大的负数约等于 0，很大的正数约等于 1。

一个简单的例子

假设我们有一个神经元，激活函数就是 S 型函数，其参数如下：

$$ w=[0,1] $$$$ b=4 $$

$w=[0, 1]$ 就是以向量的形式表示 $w_{1}=0, w_{2}=1$。现在，我们给这个神经元一个输入 $x=[2, 3]$。我们用点积来表示：

$$ \begin{align*} (w× x)+b & = ((w_{1}× x_{1})+(w_{2}× x_{2}))+b \\ & = 0× 2+1× 3+4 \\ & = 7 \end{align*} $$$$ \begin{align*} y & = f(w× x+b) \\ & = f(7) \\ & = 0.999 \end{align*} $$

当输入是 $[2, 3]$ 时，这个神经元的输出是 0.999。给定输入，得到输出的过程被称为前馈（feedforward）。

编码一个神经元

让我们来实现一个神经元！用Python的NumPy库来完成其中的数学计算：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
import numpy as np

def sigmoid(x):
  # Our activation function: f(x) = 1 / (1 + e^(-x))
  return 1 / (1 + np.exp(-x))

class Neuron:
  def __init__(self, weights, bias):
    self.weights = weights
    self.bias = bias

  def feedforward(self, inputs):
    # Weight inputs, add bias, then use the activation function
    total = np.dot(self.weights, inputs) + self.bias
    return sigmoid(total)

weights = np.array([0, 1]) # w1 = 0, w2 = 1
bias = 4                   # b = 4
n = Neuron(weights, bias)

x = np.array([2, 3])       # x1 = 2, x2 = 3
print(n.feedforward(x))    # 0.9990889488055994

还记得这个数字吗？就是我们前面算出来的例子中的0.999。

把神经元组装成网络

所谓的神经网络就是一堆神经元。这就是一个简单的神经网络：

这个网络有两个输入，一个有两个神经元（ $ℎ_{1}$ 和 $ℎ_{2}$ ）的隐藏层，以及一个有一个神经元（ $o_{1}$ ）的输出层。要注意，$o_{1}$ 的输入就是 $ℎ_{1}$ 和 ℎ_{2}$ 的输出，这样就组成了一个网络。

隐藏层就是输入层和输出层之间的层，隐藏层可以是多层的。

例子：前馈

我们继续用前面图中的网络，假设每个神经元的权重都是 $𝑤=[0,1]$ ，截距项也相同 $𝑏=0$，激活函数也都是S型函数。分别用 $ℎ_{1},ℎ_{2},o_{1}$ 表示相应的神经元的输出。

当输入 $𝑥=[2,3]$ 时，会得到什么结果？

$$ \begin{align*} ℎ_{1} & =ℎ_{2} \\ & =𝑓(𝑤× 𝑥+𝑏) \\ & =𝑓(0\times 2+1\times 3+0) \\ & =𝑓(3) \\ & =0.9526 \end{align*} $$$$ \begin{align*} o_{1} & =𝑓(𝑤×[ℎ_{1},ℎ_{2}]+𝑏) \\ & =𝑓(0× ℎ_{1}+1× ℎ_{2}+0) \\ & =𝑓(0.9526) \\ & =0.7216 \end{align*} $$

这个神经网络对输入 $[2,3]$ 的输出是0.7216，很简单。

一个神经网络的层数以及每一层中的神经元数量都是任意的。基本逻辑都一样：输入在神经网络中向前传输，最终得到输出。接下来，我们会继续使用前面的这个网络。

编码神经网络：前馈

接下来我们实现这个神经网络的前馈机制，还是这个图：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
import numpy as np

# ... code from previous section here

class OurNeuralNetwork:
  '''
  A neural network with:
    - 2 inputs
    - a hidden layer with 2 neurons (h1, h2)
    - an output layer with 1 neuron (o1)
  Each neuron has the same weights and bias:
    - w = [0, 1]
    - b = 0
  '''
  def __init__(self):
    weights = np.array([0, 1])
    bias = 0

    # The Neuron class here is from the previous section
    self.h1 = Neuron(weights, bias)
    self.h2 = Neuron(weights, bias)
    self.o1 = Neuron(weights, bias)

  def feedforward(self, x):
    out_h1 = self.h1.feedforward(x)
    out_h2 = self.h2.feedforward(x)

    # The inputs for o1 are the outputs from h1 and h2
    out_o1 = self.o1.feedforward(np.array([out_h1, out_h2]))

    return out_o1

network = OurNeuralNetwork()
x = np.array([2, 3])
print(network.feedforward(x)) # 0.7216325609518421

结果正确，看上去没问题。

训练神经网络，第1部分

现在有这样的数据：

Name	Weight (lb)	Height (in)	Gender
Alice	133	65	F
Bob	160	72	M
Charlie	152	70	M
Diana	120	60	F

接下来我们用这个数据来训练神经网络的权重和截距项，从而可以根据身高体重预测性别：

我们用0和1分别表示男性（M）和女性（F），并对数值做了转化：

Name	Weight (minus 135)	Height (minus 66)	Gender
Alice	-2	-1	1
Bob	25	6	0
Charlie	17	4	0
Diana	-15	-6	1

我这里是随意选取了135和66来标准化数据，通常会使用平均值。

损失

在训练网络之前，我们需要量化当前的网络是『好』还是『坏』，从而可以寻找更好的网络。这就是定义损失的目的。

$$ MSE= \frac{1}{n}\sum_{i=1}^{n} (y_{true}−y_{pred}) ^{2} $$

让我们仔细看看：

$n$ 是样品数，这里等于4（Alice、Bob、Charlie和Diana）。
$y$ 表示要预测的变量，这里是性别。
$y_{true}$ 是变量的真实值（『正确答案』）。例如，Alice的 $y_{true}$ 就是1（男性）。
$y_{pred}$ 是变量的预测值。这就是我们网络的输出。

$(y_{true}−y_{pred}) ^{2}$ 被称为方差（squared error）。我们的损失函数就是所有方差的平均值。预测效果越好，损失就越少。

更好的预测 = 更少的损失！

训练网络 = 最小化它的损失。

损失计算例子

假设我们的网络总是输出0，换言之就是认为所有人都是男性。损失如何？

Name	$y_{true}$	$(y_{true}−y_{pred}) ^{2}$
Alice	1	1
Bob	0	0
Charlie	0	0
Diana	1	1

$$ 𝑀𝑆𝐸=\frac{1}{4}(1+0+0+1)=0.5 $$

代码：MSE损失

下面是计算 MSE 损失的代码：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
import numpy as np

def mse_loss(y_true, y_pred):
  # y_true and y_pred are numpy arrays of the same length.
  return ((y_true - y_pred) ** 2).mean()

y_true = np.array([1, 0, 0, 1])
y_pred = np.array([0, 0, 0, 0])

print(mse_loss(y_true, y_pred)) # 0.5

如果你不理解这段代码，可以看看 NumPy 的快速入门中关于数组的操作。

好的，继续。

训练神经网络，第2部分

现在我们有了一个明确的目标：最小化神经网络的损失。通过调整网络的权重和截距项，我们可以改变其预测结果，但如何才能逐步地减少损失？

这一段内容涉及到多元微积分，如果不熟悉微积分的话，可以跳过这些数学内容。

为了简化问题，假设我们的数据集中只有Alice：

Name	Weight (minus 135)	Height (minus 66)	Gender
Alice	-2	-1	1

那均方差损失就只是Alice的方差：

$$ \begin{align*} MSE & = \frac{1}{1}\sum_{i=1}^{1} (y_{true}−y_{pred}) ^{2} \\ & =(y_{true}−y_{pred}) ^{2} \\ & =(1−y_{pred}) ^{2} \end{align*} $$

也可以把损失看成是权重和截距项的函数。让我们给网络标上权重和截距项：

这样我们就可以把网络的损失表示为：

$$ 𝐿(𝑤_{1},𝑤_{2},𝑤_{3},𝑤_{4},𝑤_{5},𝑤_{6},𝑏_{1},𝑏_{2},𝑏_{3}) $$

假设我们要优化 $𝑤_{1}$ ，当我们改变 $𝑤_{1}$ 时，损失 $𝐿$ 会怎么变化？可以用 $\frac{\partial L}{\partial 𝑤_{1}}$ 来回答这个问题，怎么计算？

接下来的数据稍微有点复杂，别担心，准备好纸和笔。

首先，让我们用 $\frac{\partial y_{pred}}{\partial𝑤_{1}}$ 来改写这个偏导数：

$$ \frac{\partial L}{\partial 𝑤_{1}}=\frac{\partial L}{\partial y_{pred}} × \frac{\partial y_{pred}}{\partial𝑤_{1}} $$

因为我们已经知道 $𝐿=(1−y_{pred}) ^{2}$，所以我们可以计算 $\frac{\partial L}{\partial y_{pred}}$ ：

$$ \begin{align*} \frac{\partial L}{\partial y_{pred}} & =\frac{\partial (1−y_{pred}) ^{2}}{\partial y_{pred}} \\ & =-2(1−y_{pred}) \end{align*} $$

现在让我们来搞定 $\frac{\partial y_{pred}}{\partial𝑤_{1}}$。 $ℎ_{1},ℎ_{2},o_{1}$ 分别是其所表示的神经元的输出，我们有：

$$ \begin{align*} y_{pred} & =o_{1} \\ & =𝑓(𝑤_{5}ℎ_{1}+𝑤_{6}ℎ_{2}+𝑏_{3}) \end{align*} $$

由于 $𝑤_{1}$ 只会影响 $ℎ_{1}$（不会影响 $ℎ_{2}$），所以：

$$ \frac{\partial y_{pred}}{\partial 𝑤_{1}}=\frac{\partial y_{pred}}{\partial h_{1}}× \frac{\partial h_{1}}{\partial𝑤_{1}} $$$$ \frac{\partial y_{pred}}{\partial h_{1}}=𝑤_{5}× f'(𝑤_{5}ℎ_{1}+𝑤_{6}ℎ_{2}+𝑏_{3}) $$$$ ℎ_{1}=𝑓(𝑤_{1}x_{1}+𝑤_{2}x_{2}+𝑏_{1}) $$$$ \frac{\partial h_{1}}{\partial𝑤_{1}}=x_{1}× f'(𝑤_{1}x_{1}+𝑤_{2}x_{2}+𝑏_{1}) $$

在这里， $x_{1}$ 是身高， $x_{2}$ 是体重。这是我们第二次看到 $𝑓′(𝑥)$ （S 型函数的导数）了。求解：

$$ 𝑓(𝑥)=\cfrac{1}{ 1 + e^{-x} } $$$$ \begin{align*} 𝑓′(𝑥) & =\cfrac{e^{-x}}{ (1 + e^{-x})^{2}} \\ & =𝑓(𝑥)× (1-𝑓(𝑥)) \end{align*} $$

稍后我们会用到这个 $𝑓′(𝑥)$ 。

我们已经把 $\frac{\partial L}{\partial 𝑤_{1}}$ 分解成了几个我们能计算的部分：

$$ \frac{\partial L}{\partial 𝑤_{1}}=\frac{\partial L}{\partial y_{pred}} × \frac{\partial y_{pred}}{\partial h_{1}}× \frac{\partial h_{1}}{\partial𝑤_{1}} $$

这种计算偏导的方法叫『反向传播算法』(backpropagation)。

好多数学符号，如果你还没搞明白的话，我们来看一个实际例子。

例子：计算偏导数

我们还是看数据集中只有Alice的情况：

Name	Weight (minus 135)	Height (minus 66)	Gender
Alice	-2	-1	1

把所有的权重和截距项都分别初始化为 1 和 0。在网络中做前馈计算：

$$ \begin{align*} ℎ_{1} & =𝑓(𝑤_{1}x_{1}+𝑤_{2}x_{2}+𝑏_{1}) \\ & =𝑓(−2+−1+0) \\ & =0.0474 \end{align*} $$$$ \begin{align*} ℎ_{2} & =𝑓(𝑤_{3}x_{1}+𝑤_{4}x_{2}+𝑏_{2}) \\ & =0.0474 \end{align*} $$$$ \begin{align*} 𝑜_{1} & =𝑓(𝑤_{5}ℎ_{1}+𝑤_{6}ℎ_{2}+𝑏_{3}) \\ & =𝑓(0.0474+0.0474+0) \\ & =0.524 \end{align*} $$$$ \frac{\partial L}{\partial 𝑤_{1}}=\frac{\partial L}{\partial y_{pred}} × \frac{\partial y_{pred}}{\partial h_{1}}× \frac{\partial h_{1}}{\partial𝑤_{1}} $$$$ \begin{align*} \frac{\partial L}{\partial y_{pred}} & =−2(1−y_{pred}) \\ & =−2(1−0.524) \\ & =−0.952 \end{align*} $$$$ \begin{align*} \frac{\partial y_{pred}}{\partial h_{1}} & =𝑤_{5}× f'(𝑤_{5}ℎ_{1}+𝑤_{6}ℎ_{2}+𝑏_{3}) \\ & =1×𝑓′(0.0474+0.0474+0) \\ & =𝑓(0.0948)(1−𝑓(0.0948)) \\ & =0.249 \end{align*} $$$$ \begin{align*} \frac{\partial h_{1}}{\partial𝑤_{1}} & =x_{1}× f'(𝑤_{1}x_{1}+𝑤_{2}x_{2}+𝑏_{1}) \\& =−2×𝑓′(−2+−1+0) \\& =−2𝑓(−3)(1−𝑓(−3)) \\& =−0.0904 \end{align*} $$$$ \begin{align*} \frac{\partial L}{\partial 𝑤_{1}} & =−0.952×0.249×−0.0904 \\ & =0.0214 \end{align*} $$

提示：前面已经得到了 S 型激活函数的导数 $𝑓′(𝑥)=𝑓(𝑥)×(1−𝑓(𝑥))$ 。

搞定！这个结果的意思就是增加 $𝑤_{1}$ ， $𝐿$ 也会随之轻微上升。

训练：随机梯度下降

现在训练神经网络已经万事俱备了！我们会使用名为随机梯度下降法的优化算法来优化网络的权重和截距项，实现损失的最小化。核心就是这个更新灯饰：

$$ 𝑤_{1}←𝑤_{1}−𝜂\frac{\partial L}{\partial 𝑤_{1}} $$

𝜂 是一个常数，被称为学习率，用于调整训练的速度。我们要做的就是用 $𝑤_{1}$ 减去 $𝜂\frac{\partial L}{\partial 𝑤_{1}}$ ：

如果 $\frac{\partial L}{\partial 𝑤_{1}}$ 是正数， $𝑤_{1}$ 会变小， $𝐿$ 会下降。
如果 $\frac{\partial L}{\partial 𝑤_{1}}$ 是负数， $𝑤_{1}$ 会变大， $𝐿$ 会上升。

如果我们对网络中的每个权重和截距项都这样进行优化，损失就会不断下降，网络性能会不断上升。

我们的训练过程是这样的： 1. 从我们的数据集中选择一个样本，用随机梯度下降法进行优化——每次我们都只针对一个样本进行优化； 2. 计算每个权重或截距项对损失的偏导（例如 $\frac{\partial L}{\partial 𝑤_{1}}$ 、 $\frac{\partial L}{\partial 𝑤_{2}}$等）； 3. 用更新等式更新每个权重和截距项； 4. 重复第一步；

代码：一个完整的神经网络

我们终于可以实现一个完整的神经网络了：

Name	Weight (minus 135)	Height (minus 66)	Gender
Alice	-2	-1	1
Bob	25	6	0
Charlie	17	4	0
Diana	-15	-6	1

  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
import numpy as np

def sigmoid(x):
  # Sigmoid activation function: f(x) = 1 / (1 + e^(-x))
  return 1 / (1 + np.exp(-x))

def deriv_sigmoid(x):
  # Derivative of sigmoid: f'(x) = f(x) * (1 - f(x))
  fx = sigmoid(x)
  return fx * (1 - fx)

def mse_loss(y_true, y_pred):
  # y_true and y_pred are numpy arrays of the same length.
  return ((y_true - y_pred) ** 2).mean()

class OurNeuralNetwork:
  '''
  A neural network with:
    - 2 inputs
    - a hidden layer with 2 neurons (h1, h2)
    - an output layer with 1 neuron (o1)

  *** DISCLAIMER ***:
  The code below is intended to be simple and educational, NOT optimal.
  Real neural net code looks nothing like this. DO NOT use this code.
  Instead, read/run it to understand how this specific network works.
  '''
  def __init__(self):
    # 权重，Weights
    self.w1 = np.random.normal()
    self.w2 = np.random.normal()
    self.w3 = np.random.normal()
    self.w4 = np.random.normal()
    self.w5 = np.random.normal()
    self.w6 = np.random.normal()

    # 截距项，Biases
    self.b1 = np.random.normal()
    self.b2 = np.random.normal()
    self.b3 = np.random.normal()

  def feedforward(self, x):
    # x is a numpy array with 2 elements.
    h1 = sigmoid(self.w1 * x[0] + self.w2 * x[1] + self.b1)
    h2 = sigmoid(self.w3 * x[0] + self.w4 * x[1] + self.b2)
    o1 = sigmoid(self.w5 * h1 + self.w6 * h2 + self.b3)
    return o1

  def train(self, data, all_y_trues):
    '''
    - data is a (n x 2) numpy array, n = # of samples in the dataset.
    - all_y_trues is a numpy array with n elements.
      Elements in all_y_trues correspond to those in data.
    '''
    learn_rate = 0.1
    epochs = 1000 # number of times to loop through the entire dataset

    for epoch in range(epochs):
      for x, y_true in zip(data, all_y_trues):
        # --- Do a feedforward (we'll need these values later)
        sum_h1 = self.w1 * x[0] + self.w2 * x[1] + self.b1
        h1 = sigmoid(sum_h1)

        sum_h2 = self.w3 * x[0] + self.w4 * x[1] + self.b2
        h2 = sigmoid(sum_h2)

        sum_o1 = self.w5 * h1 + self.w6 * h2 + self.b3
        o1 = sigmoid(sum_o1)
        y_pred = o1

        # --- Calculate partial derivatives.
        # --- Naming: d_L_d_w1 represents "partial L / partial w1"
        d_L_d_ypred = -2 * (y_true - y_pred)

        # Neuron o1
        d_ypred_d_w5 = h1 * deriv_sigmoid(sum_o1)
        d_ypred_d_w6 = h2 * deriv_sigmoid(sum_o1)
        d_ypred_d_b3 = deriv_sigmoid(sum_o1)

        d_ypred_d_h1 = self.w5 * deriv_sigmoid(sum_o1)
        d_ypred_d_h2 = self.w6 * deriv_sigmoid(sum_o1)

        # Neuron h1
        d_h1_d_w1 = x[0] * deriv_sigmoid(sum_h1)
        d_h1_d_w2 = x[1] * deriv_sigmoid(sum_h1)
        d_h1_d_b1 = deriv_sigmoid(sum_h1)

        # Neuron h2
        d_h2_d_w3 = x[0] * deriv_sigmoid(sum_h2)
        d_h2_d_w4 = x[1] * deriv_sigmoid(sum_h2)
        d_h2_d_b2 = deriv_sigmoid(sum_h2)

        # --- Update weights and biases
        # Neuron h1
        self.w1 -= learn_rate * d_L_d_ypred * d_ypred_d_h1 * d_h1_d_w1
        self.w2 -= learn_rate * d_L_d_ypred * d_ypred_d_h1 * d_h1_d_w2
        self.b1 -= learn_rate * d_L_d_ypred * d_ypred_d_h1 * d_h1_d_b1

        # Neuron h2
        self.w3 -= learn_rate * d_L_d_ypred * d_ypred_d_h2 * d_h2_d_w3
        self.w4 -= learn_rate * d_L_d_ypred * d_ypred_d_h2 * d_h2_d_w4
        self.b2 -= learn_rate * d_L_d_ypred * d_ypred_d_h2 * d_h2_d_b2

        # Neuron o1
        self.w5 -= learn_rate * d_L_d_ypred * d_ypred_d_w5
        self.w6 -= learn_rate * d_L_d_ypred * d_ypred_d_w6
        self.b3 -= learn_rate * d_L_d_ypred * d_ypred_d_b3

      # --- Calculate total loss at the end of each epoch
      if epoch % 10 == 0:
        y_preds = np.apply_along_axis(self.feedforward, 1, data)
        loss = mse_loss(all_y_trues, y_preds)
        print("Epoch %d loss: %.3f" % (epoch, loss))

# Define dataset
data = np.array([
  [-2, -1],  # Alice
  [25, 6],   # Bob
  [17, 4],   # Charlie
  [-15, -6], # Diana
])
all_y_trues = np.array([
  1, # Alice
  0, # Bob
  0, # Charlie
  1, # Diana
])

# Train our neural network!
network = OurNeuralNetwork()
network.train(data, all_y_trues)

随着网络的学习，损失在稳步下降。

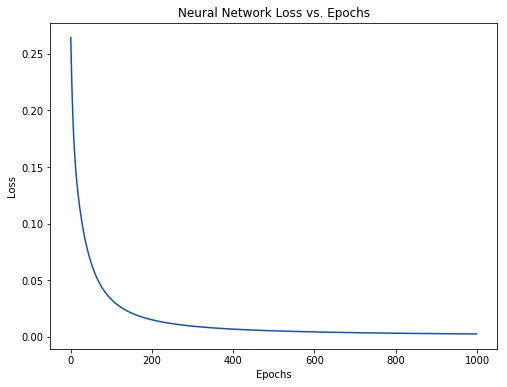
现在我们可以用这个网络来预测性别了：

1
2
3
4
5
# Make some predictions
emily = np.array([-7, -3]) # 128 pounds, 63 inches
frank = np.array([20, 2])  # 155 pounds, 68 inches
print("Emily: %.3f" % network.feedforward(emily)) # 0.951 - F
print("Frank: %.3f" % network.feedforward(frank)) # 0.039 - M

接下来？

搞定了一个简单的神经网络，快速回顾一下：

介绍了神经网络的基本结构——神经元；
在神经元中使用S型激活函数；
神经网络就是连接在一起的神经元；
构建了一个数据集，输入（或特征）是体重和身高，输出（或标签）是性别；
学习了损失函数和均方差损失；
训练网络就是最小化其损失；
用反向传播方法计算偏导；
用随机梯度下降法训练网络；

接下来你还可以：

用机器学习库实现更大更好的神经网络，例如TensorFlow、Keras和PyTorch；
在浏览器中实现神经网络；
其他类型的激活函数；
其他类型的优化器；
学习卷积神经网络，这给计算机视觉领域带来了革命；
学习递归神经网络，常用语自然语言处理；

版权声明
本文作者：Fermi
本文链接：https://fermi.ink/posts/2024/07/04/02/
转载标题：【转载】用 Python 从头实现神经网络 —— Fermi
许可说明：本站所有文章除特别声明外均为博主原创作品，遵循知识共享（CC BY-NC-SA 4.0）许可协议进行许可。非商业转载请注明原文出处（作者，原文链接）和本声明！商业转载请联系作者获得授权。